Interferencias


Cuando en un punto del espacio coinciden dos o más ondas se produce una interferencia. Vamos a estudiar cómo es la onda resultante en una interferencia de ondas armónicas.

Principio de superposición

Este principio dice:

Cuando en un medio coinciden dos o más ondas el desplazamiento de cada punto del medio es la suma de los desplazamientos que provocaría cada una de las ondas por separado:

y(x,t) = y1 (x, t) + y2 (x, t) + .. + yn (x, t)


Para aplicar este principio nos será muy útil conocer la siguiente relación matemática:

Supongamos que tenemos dos focos F1 y F2 que emiten ondas armónicas de la misma frecuencia y longitud de onda pero que no emiten en fase, con lo que la constante de fase para cada onda es distinta (φ1 y φ2 respectivamente). En términos generales las ondas recorrerán distancias distintas hasta que coincidan en el punto P. Las funciones de onda para cada foco son:



La función de onda resultante y(x, t) en el punto P la obtenemos aplicando el principio de superposición y la relación matemática anterior: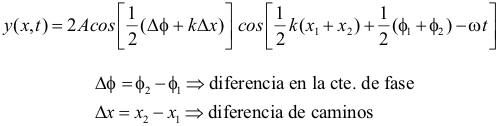

Se observa que el resultado es otra onda armónica de la misma frecuencia y longitud de onda que las que interfieren, pero cuya amplitud (A´) viene dada por la expresión:


es decir, depende de la diferencia de la constante de fase Δφ y de la diferencia de caminos recorridos por cada onda Δx.

En esta animación puedes variar la longitud de onda y el desfase entre las ondas generadas por dos focos y ver la onda que se genera de su interferencia. También puedes desplazar el foco F2 para ver cómo afecta la diferencia de caminos.

Diferencia de caminos

Como ejemplo, analizaremos matemáticamente ahora el caso en el que los focos emiten en fase, es decir Δφ es nulo, pero las ondas recorren caminos distintos. La amplitud resultante es entonces:



  • Interferencia constructiva: se produce cuando la amplitud resultante es máxima, es decir, vale A' = 2A. Esto sucede para:


    Es decir, cuando la diferencia de caminos recorridos por las ondas es un múltiplo entero de la longitud de onda, la onda resultante tiene el doble de amplitud que las que interfieren.

  • Interferencia destructiva: se produce cuando se anula el coseno, entonces la amplitud resultante es mínima, es decir, vale A' = 0. Esto sucede para:



    • Es decir, cuando la diferencia de caminos recorridos por las ondas es un múltiplo impar de media longitud de onda, la onda resultante es nula.