Problemas resueltos


1.- Un electrón de carga q = -1.6 10-19 C se mueve con una velocidad v = 0.5 105 i + 0.5 105 j (m/s). En el momento en que pasa por el punto de coordenadas (1, 1) calcular:

  1. el campo magnético B que el electrón crea en los puntos (-1, -1) y (0, 2). (Pincha para ver el resultado).
  2. la fuerza que sufre un protón situado en el punto (0, 2) si lleva una velocidad:

    1) v = 2 105 k (m/s).

    2) v = 2 105 j (m/s).

    (Pincha para ver el resultado).

Datos: μo = 4 π 10-7 Tm/A; coordenadas en metros.

Resolución del problema en pdf



2.- Una bobina formada por 30 espiras circulares está situada en una zona del espacio donde exite un campo magnético B = 2 i (T), de modo que el vector S que representa la superficie de las espiras forma un ángulo Φ = 30º con el vector B. El radio de la bobina es r = 10 cm y por ella circula una corriente I = 0.05 A.

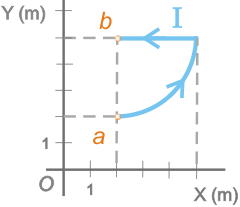
  1. Determinar el vector momento magnético de la bobina. (Pincha para ver el resultado).
  2. Calcular el momento de las fuerzas que el campo magnético ejerce sobre la bobina. ¿Hacia dónde tiende a girar la bobina? (Pincha para ver el resultado).

Resolución del problema en pdf



3.- Se dispone de un hilo conductor por el que circula una corriente de intensidad I = 3 A, formado por un cuadrante circular y un segmento horizontal, según la figura (a,b). El conductor se encuentra en un campo magnético uniforme B = 2 10- 3 i - 5 10- 3 k (T).

  1. Calcular el vector fuerza que el campo magnético B ejerce sobre el conductor. (Pincha para ver el resultado).
  2. Si se cerrase el conductor con un segmento vertical desde el punto b al punto a ¿cuánto valdría entonces la fuerza ejercida por B sobre la espira resultante? Calcular el momento magnético de la espira y el momento de la fuerza que B ejerce sobre la misma. (Pincha para ver el resultado).

Resolución del problema en pdf



4.- Una partícula de carga q = - 1.6 10- 19 C y masa m = 1.7 10- 27 kg entra con una velocidad v = v i en una región del espacio en la que existe un campo magnético uniforme B = - 0.5 k (T). El radio de la trayectoria circular que describe es R = 0.3 m.


  1. Dibujar la fuerza que ejerce el campo sobre la partícula en el instante inicial y la trayectoria que sigue ésta. Calcular la velocidad v con la que entró a partir de la Segunda Ley de Newton en el eje normal. (Pincha para ver el resultado).
  2. Calcular el periodo del movimiento y la frecuencia angular ω. ¿Cómo varían el radio de la trayectoria y el periodo del movimiento si se duplica la velocidad de entrada? (Pincha para ver el resultado).
  3. ¿Cuánto vale la energía cinética cuando entra la partícula en el campo magnético? ¿Y después de dar una vuelta completa? (Pincha para ver el resultado).

Resolución del problema en pdf