Ondas estacionariasNodos y antinodosCuando la interferencia se produce entre dos ondas que viajan en sentidos opuestos se puede generar una onda estacionaria. Esto sucede por ejemplo en el caso de que una onda encuentre un obstáculo, se refleje e interfiera con la onda incidente. Las funciones de onda de la onda incidente y reflejada serán:  Si aplicamos el principio de superposición la onda resultante tendrá la forma:  Se observa que esta función no representa una onda que se desplaza: cada elemento de la cuerda (dando valores fijos a x) describe un movimiento armónico simple en la dirección vertical de amplitud A´.  Los puntos de coordenada x para los que el desplazamiento vertical es siempre nulo se llaman nodos y aquellos para los que la amplitud es máxima antinodos. La condición que deben cumplir los nodos es entonces: 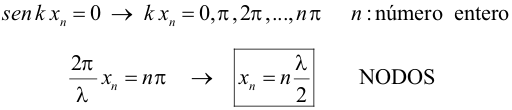 Para los antinodos la condición es: 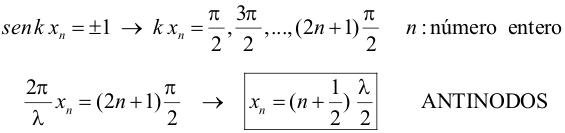 Tanto los nodos como los antinodos consecutivos están separados una distancia igual a media longitud de onda. Cuerda fija por ambos extremosEn esta animación se muestra cómo se genera una onda estacionaria en una cuerda fija por los dos extremos. En este caso no todas las longitudes de onda generan ondas estacionarias, ya que ambos extremos deben ser nodos. Las frecuencias asociadas a la longitudes de onda permitidas se llaman frecuencias naturales o de resonancia. Si la cuerda tiene una longitud L, aplicamos la condición de que el punto de coordenada x = L debe ser un nodo:  Recordando la relación entre la velocidad de propagación (v), que depende del medio y la frecuencia de la onda (f):
El valor de la frecuencia para n = 1 se denomina frecuencia fundamental o primer armónico y le corresponde una longitud de onda igual a 2L:  Las sucesivas frecuencias de resonancia son múltiplos enteros de la frecuencia fundamental. Si las ondas que son de una frecuencia que no cumple esta condición no se generan ondas estacionarias. |



