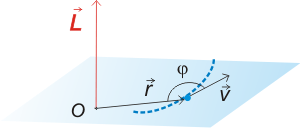
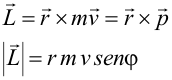Momento angular de una partícula

Consideremos una partícula de masa m que se mueve con respecto a O con una velocidad v. Definimos una nueva magnitud vectorial, llamada momento angular de la partícula con respecto a O (L):

Sus unidades son: m²kg/s. El vector L es en cada instante perpendicular al plano formado por el vector posición y el vector velocidad; cuando la trayectoria es plana y el origen está contenido en el plano de la misma, L es perpendicular a dicho plano.

Teorema de conservación

Para determinar bajo qué condiciones L se mantiene constante, derivamos con respecto al tiempo:

El primer término es nulo por tratarse del producto vectorial de dos vectores paralelos, con lo que aplicando la definición de fuerza dada en la segunda ley de Newton queda:

Este producto vectorial se denomina momento o torque de una fuerza (τ) con respecto al origen O:

el vector L será constante cuando su derivada sea nula. Esto constituye el Teorema de Conservación del Momento Angular:

Esta condición se cumple en dos casos:

• en el caso de una partícula libre, la fuerza a la que está sometida es nula por lo que no ejerce momento y por tanto se mueve con L constante, además de con momento lineal constante
• cuando el vector posición es paralelo a la fuerza, el producto vectorial es nulo por lo que L también es constante. Esto sucede en el caso de una fuerza central, es decir, que pasa siempre por un punto fijo: el momento angular de una partícula sometida exclusivamente a una fuerza central es constante. La fuerza gravitatoria es una fuerza central por lo que, por ejemplo, la Tierra se mueve con respecto al Sol con L constante. Si consultas la sección ¿sabías que..? de esta página verás qué consecuencias tiene este hecho.