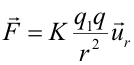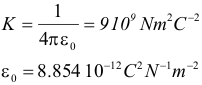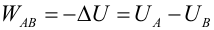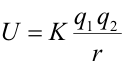Fuerza electrostática. Energía potencial

Sean las dos cargas puntuales q₁ y q separadas una distancia r, que se encuentran en reposo con respecto al origen O del sistema de referencia inercial. La fuerza que la carga q₁ ejerce sobre q se denomina fuerza electrostática y viene dada por la ley de Coulomb:

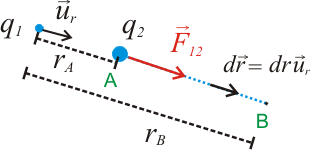
donde K es una constante denominada constante electrostática que depende del medio y ε₀ es la permitividad eléctrica del vacío.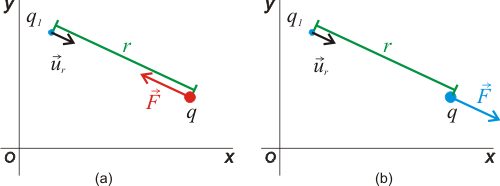

El vector u_r es un vector unitario que va desde la carga q₁ a la carga q de modo que cuando ambas cargas tienen distinto signo (figura (a)) la fuerza electrostática es de atracción, mientras que si tienen el mismo signo la fuerza electrostática es de repulsión (figura (b)).

Al estudiar problemas de cargas en electrostática, se denomina carga fuente a la carga que ejerce la fuerza (en este caso q₁) y carga testigo o carga de prueba a la carga sobre la que se calcula la fuerza (q).

La fuerza electrostática cumple la tercera ley de Newton, por lo que la carga q₁ experimentará una fuerza de igual módulo y sentido contrario que la que experimenta q.

Si la carga q₁ se encontrase en presencia de N cargas puntuales, la fuerza total sobre ella sería la resultante de todas las fuerzas que ejercen sobre ella las N cargas.

Energía potencial electrostática

La ley de Coulomb es formalmente igual a la ley de Gravitación Universal de Newton, que permite calcular la fuerza de atracción entre dos masas. Al igual que esta última, la fuerza electrostática dada por la ley de Coulomb es una fuerza conservativa. Por tanto, el trabajo es independiente de la trayectoria y se puede calcular a partir de una función escalar denominada energía potencia electrostática U.

Supongamos que bajo la acción de la fuerza electrostática la carga de prueba q₂ se desplaza desde un punto A a un punto B, entonces el trabajo W realizado por la fuerza es:

Cuando se encuentra bajo la única acción de la fuerza electrostática la carga de prueba se moverá siempre en el sentido en el que disminuye su energía potencial (U_A > U_B); de este modo el trabajo de la fuerza es positivo, es decir, corresponde a una fuerza que va en el mismo sentido del movimiento.

Por otra parte, si aplicamos la definición de trabajo a la fuerza electrostática expresando ésta a partir de la Ley de Coulomb, se obtiene: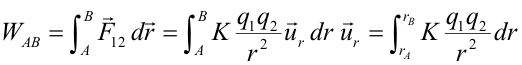

Integrando: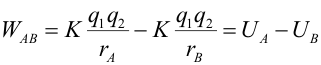

lo que, comparando con la expresión inicial para el trabajo, nos permite identificar la variación de energía potencial.

De forma general se toma como origen para la energía potencial el infinito, de modo que cuando la distancia entre las dos cargas es infinita, la energía potencial entre ambas es nula. Por tanto, la energía potencial de un sistema de dos cargas puntuales q₁ y q₂ que están separadas una distancia r es:

Cuando una carga q se encuentra en presencia de N cargas puntuales, la energía potencial total se calcula a partir del sumatorio: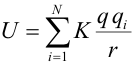

Conocida la expresión de la energía potencial se puede obtener la fuerza a partir del operador gradiente. Si lo aplicamos al caso de dos cargas: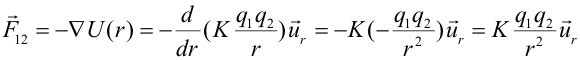

que es la expresión de la fuerza dada por la Ley de Coulomb.