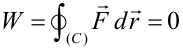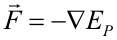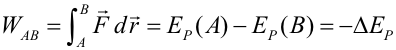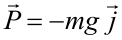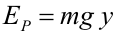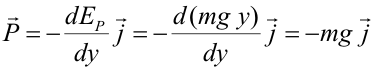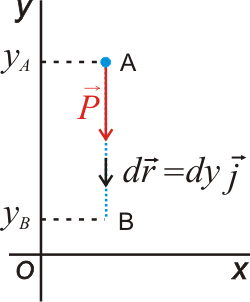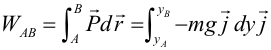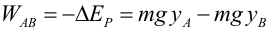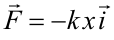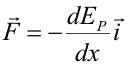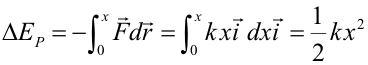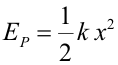Fuerzas conservativas. Energía potencial

Fuerzas conservativas

Una fuerza conservativa es aquella cuyo trabajo depende únicamente de las posiciones inicial y final de la partícula y no de la trayectoria que ésta ha descrito para ir desde la posición inicial a la final.

Una consecuencia de este hecho es que el trabajo de una fuerza conservativa a lo largo de una trayectoria cerrada es cero:

Si el trabajo de una fuerza conservativca no depende del camino seguido por la partícula y el punto final coincide con el inicial, el trabajo de dicha fuerza es cero.

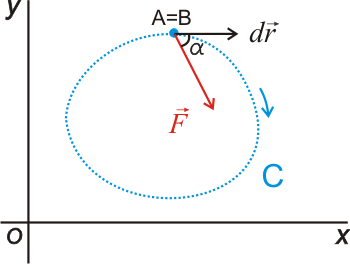
Utilizando la descomposición de Helmholtz una fuerza conservativa puede ser escrita como el gradiente de una función escalar cambiado de signo:

Dicha función escalar se denomina energía potencial, y sólo depende de las coordenadas.

Las fuerzas conservativas son muy importantes en Física, ya que fuerzas como la gravitatoria o la elástica son conservativas. Como veremos a continuación, cada una de estas fuerzas lleva asociada su propia energía potencial.

Puede demostrarse (con ayuda del teorema fundamental de las integrales de línea) que el trabajo de una fuerza conservativa viene dado por:

Las unidades de energía potencial en el Sistema Internacional son los julios (J).

Energía potencial asociada a algunas fuerzas conservativas

Fuerza constante (peso)

Cualquier fuerza constante es una fuerza conservativa. Como ejemplo de fuerza constante trataremos el peso, es decir, la fuerza gravitatoria cerca de la superficie de la Tierra.

Como vimos en el apartado Ejemplos de fuerzas, el peso es una fuerza constante que apunta hacia el centro de la Tierra. Vectorialmente, el peso es:

La energía potencial asociada a dicha fuerza (energía potencial gravitatoria) es:

Ya que:

El trabajo del peso es menos la variación de su energía potencial:

Ambas formas de calcular el trabajo dan obviamente el mismo resultado.

Fuerza de un muelle

La fuerza de un muelle viene dada por la ley de Hooke:

Y su energía potencial (energía potencial elástica) tiene que ser tal que:

Integrando esta ecuación entre cero y x se obtiene la expresión para la energía potencial:

Se ha tomado nivel cero de energía potencial a la posición de equilibrio. Por tanto la energía potencial elástica asociada a la deformación x es: