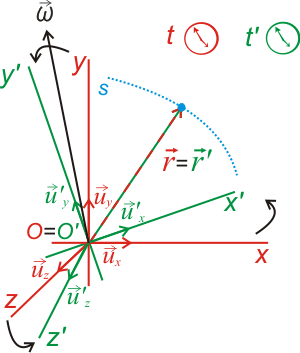
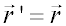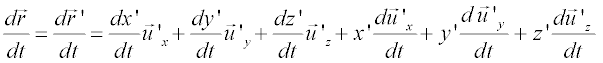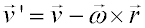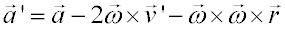Movimiento relativo (2/2)Movimiento relativo de rotación uniformeCuando dos sistemas de referencia se encuentran en movimiento relativo de rotación uniforme, cada uno de ellos mide un vector aceleración distinto cuando observan el movimiento de un mismo cuerpo. En la siguiente animación se muestra la trayectoria que describe una pelota lanzada desde el centro de un tiovivo, que rota con velocidad angular constante, desde el punto de vista de un sistema de referencia inercial en reposo en el suelo (en azul) y desde el punto de vista de un observador que se encuentra en la periferia del tiovivo (en rojo). Para el segundo, que es no inercial, la pelota describe una trayectoria curva, por lo que para él la pelota tiene aceleración. Puedes cambiar el ángulo de lanzamiento de la pelota pinchando sobre la flecha verde y arrastrándola. Para que la pelota llegue a las manos del observador de la periferia, ha de ser lanzada con un cierto ángulo con respecto a este último. A continuación se deduce la relación entre las aceleraciones medidas por ambos observadores. Vamos a suponer que uno de los sistemas de referencia (O) está en reposo y O' rota con velocidad angular ω constante con respecto a él.
En la figura anterior está representada la trayectoria de una partícula (en azul) y los dos sistemas de referencia con sus vectores unitarios. Como puede observarse,
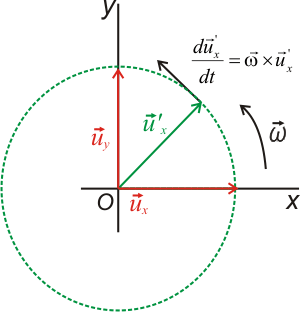
Para encontrar la relación entre las velocidades medidas por ambos observadores debemos derivar la ecuación anterior. Al hacer esta derivada es necesario tener en cuenta que los vectores unitarios asociados a O' giran con velocidad angular ω con respecto a O, por lo que no son constantes. Sus derivadas están representadas en la parte derecha de la figura anterior. Teniendo en cuenta este hecho, Por lo que:
Derivando de nuevo repitiendo el mismo procedimiento,
|