Vectores constituyentes

Vector unitario

Un vector unitario es aquél que tiene módulo 1. Para hallar un vector unitario a partir de cualquier vector, hay que dividir este último por su módulo.

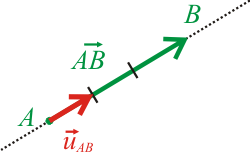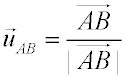
AB mide 3, por lo que: Y su módulo:

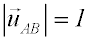
Un vector unitario puede emplearse para definir el sentido positivo de cualquier eje. Así, para los ejes cartesianos x,y,z se emplean los vectores i, j y k:

Vectores unitarios para los ejes cartesianos:

La orientación de estos tres ejes cartesianos puede cambiarse, siempre y cuando su orientación relativa sea la misma.

Del mismo modo pueden definirse un vector tangente y un vector perpendicular a una curva en cada punto, o un vector unitario en las direcciones radial y angular:

Con ayuda de estos vectores unitarios puede expresarse un vector cualquiera en función de sus vectores constituyentes.

Vectores constituyentes de un vector

Una vez introducidos los vectores unitarios i, j, k que definen los sentidos positivos de los ejes cartesianos, podemos expresar cualquier vector como la suma de los siguientes vectores:

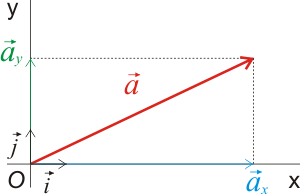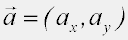
Componentes cartesianas En tres dimensiones:

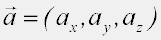
Como se observa en la figura anterior:

Y de forma análoga en tres dimensiones:

Que es la forma que más comúnmente emplearemos para expresar una magnitud vectorial.