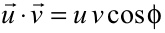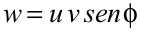Operaciones con vectoresSupongamos que tenemos dos vectores u y v expresados a partir de sus vectores constituyentes, en dos dimensiones para simplificar:  Suma de vectoresSe define el vector suma de ambos (w) a otro vector cuyas componentes se calculan sumando las componentes de cada uno de ellos.  Se puede apreciar según el dibujo que gráficamente esto equivale a colocar un vector a continuación del otro y dibujar el vector desde el origen del primero al final del segundo. Producto escalar (·)El producto escalar de dos vectores u y v que forman un ángulo φ se define como:
De la expresión anterior se observa que el producto escalar de dos vectores no es un vector, es un número (un escalar). Además el producto escalar de dos vectores perpendiculares es nulo. Se deducen entonces los siguientes resultados: 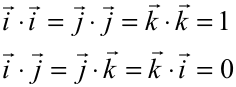
Si los vectores están expresados en componentes, en tres dimensiones y aplicando los resultados anteriores se obtiene que: 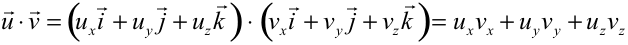 El producto escalar de dos vectores posee la propiedad conmutativa. Producto vectorial (x)El producto vectorial de dos vectores que forman un ángulo φ es otro vector, de dirección perpendicular al plano formado por los dos vectores, sentido el que da la regla de la mano derecha y módulo el que se especifica a continuación:
El producto vectorial no posee la propiedad conmutativa, ya que se cumple que:  Además, se cumple que el producto vectorial de dos vectores paralelos es nulo. Se obtienen entonces las siguientes relaciones:  Si los vectores vienen expresados en componentes el producto vectorial se calcula desarrollando el determinante:  |