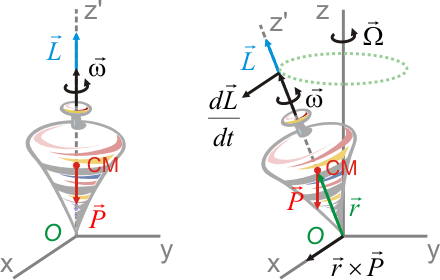
Precesión de una peonzaEl movimiento de una peonza puede ser explicado haciendo uso de la ecuación del movimiento de rotación. En la parte izquierda de la figura se ha representado una peonza situada en posición vertical que, tras ser lanzada, rota con respecto a su eje de simetría z'. Las fuerzas externas que actúan sobre ella son su peso (aplicado en el centro de masas) y la normal del suelo, que por simplicidad no está representada ya que no afecta al movimiento de rotación (en ningún caso hace momento con respecto a O).
Si la peonza estuviera siempre en posición vertical, su momento angular L permanecería constante, ya que el peso no haría momento con respecto a O. Por ser el eje de giro un eje principal L es además pararelo a dicho eje y según la ecuación del movimiento de rotación:
Es decir, en esta situación la peonza rotaría indefinidamente con velocidad angular ω constante y momento angular constante. Cuando la peonza se desvía de su posición vertical, el momento del peso con respecto a O ya no es nulo (ver parte derecha de la figura) y el momento angular varía. La variación de momento angular es igual al momento del peso y perpendicular al vector momento angular, por lo que este último variará de dirección pero no de módulo. El efecto de esta variación es que el eje de giro de la peonza empieza a su vez a rotar, describiendo una trayectoria como la representada en verde en la figura. Este movimiento se denomina precesión. El eje de rotación de la Tierra tiene un movimiento de precesión producido por el momento de la fuerza gravitatoria que sobre ella ejercen el Sol y la Luna. El eje de rotación de la Tierra tarda cerca de 26000 años en describir una rotación completa. Este fenómeno es conocido como precesión de los equinoccios. |