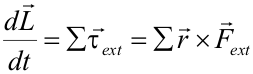Ecuación del movimiento de rotaciónEl momento angular de un sólido rígido que rota con respecto a uno de sus ejes principales de inercia (que por el momento supondremos fijo con respecto a un sistema de referencia inercial) viene dado por:
Donde I es el momento de inercia del sólido y ω es su velocidad angular. La variación del estado de rotación de un sólido viene determinada por la variación de su velocidad angular por lo que, si queremos describir el movimiento de rotación debemos encontrar una ecuación que nos permita calcular la aceleración angular del mismo. Puesto que en la expresión del momento angular aparece la velocidad angular, derivándola obtendremos la aceleración angular:
La variación del momento angular de un sistema de partículas (y, por tanto, de un sólido) es igual al momento de las fuerzas externas que actúan sobre el sistema:
Igualando ambas expresiones,
Ésta es la ecuación del movimiento de rotación de un sólido rígido que, como puede observarse, es análoga a la segunda ley de Newton. La segunda ley de Newton nos proporciona un modo de calcular la aceleración de una partícula (o del centro de masas de un sistema de partículas) conociendo las fuerzas que actúan sobre ella. La ecuación del movimiento de rotación de un sólido nos permite determinar su aceleración angular calculando el momento de las fuerzas externas que actúan sobre él. Para que un cuerpo rote (para que tenga aceleración angular) no basta con que actúen fuerzas externas sobre él, sino que estas fuerzas han de tener momento resultante no nulo. El papel que juega la masa de una partícula en la segunda ley de Newton (su inercia, es decir, la resistencia que opone a cambiar su estado de movimiento), lo desempeña ahora el momento de inercia. Despejando α, se obtiene:
Es decir, para un momento de fuerzas dado, cuanto mayor sea el momento de inercia del sólido menor será su aceleración angular, por lo que la velocidad angular del mismo variará más lentamente. El momento de inercia mide la resistencia que opone un cuerpo a variar su estado de movimiento de rotación. De la ecuación anterior se deduce que el vector aceleración angular es paralelo a la resultante de los momentos de las fuerzas externas, del mismo modo que la aceleración de una partícula es paralela a la resultante de las fuerzas que actúan sobre ella. Cuanto mayor sea el módulo de esta resultante, mayor será el módulo de la aceleración angular. En el siguiente ejemplo se analiza el movimiento de rotación de una puerta utilizando la ecuación del movimiento de rotación.
Si la fuerza se aplica en una dirección paralela al vector r la puerta no se abrirá, ya que en este caso el momento de la fuerza será nulo y no habrá aceleración angular. |