Entropía (3/3)

Aplicación a procesos irreversibles

La definición de la función entropía implica que, para poder calcular su variación entre dos estados determinados de un sistema, estos han de estar conectados por una transformación reversible. Sin embargo, hay situaciones en las que un sistema termodinámico pasa desde un estado inicial a uno final a través de una transformación irreversible. ¿Cómo se calcula la variación de entropía en estos casos? A continuación se presenta un ejemplo, la denominada expansión libre de Joule.

Expansión libre de Joule

En la siguiente figura se ha representado un recipiente aislado adiabáticamente del exterior dividido en dos compartimentos. En el compartimento de la izquierda hay un gas ideal y en el de la derecha se ha hecho el vacío. Cuando se elimina la pared central, el gas ideal se expande irreversiblemente hasta ocupar todo el volumen disponible.

¿Cuál es la variación de entropía entre los estados inicial y final del sistema? Como el recipiente está aislado del exterior, durante la transformación no se produce intercambio de calor. Tampoco se realiza trabajo, ya que el gas se expande contra el vacío. Por tanto, utilizando el primer principio de la Termodinámica:

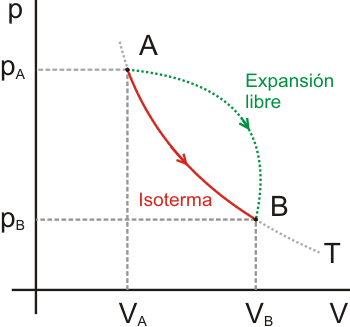
Se deduce que la temperatura inicial del gas ideal es la misma que la final. Como el calor intercambiado durante el proceso no puede utilizarse para calcular la variación de entropía (puesto que fue intercambiado irreversiblemente), se toma una transformación reversible que conecte los mismos estados inicial y final del sistema, como se muestra en rojo en la siguiente figura.

Esta transformación es una isoterma. La variación de entropía en una transformación isoterma de un gas ideal viene dada por:

Como la entropía es una función de estado, la variación de entropía entre los mismos estados inicial y final A y B sea cual sea la transformación que los una (en particular, la expansión libre) será la calculada en la expresión anterior.