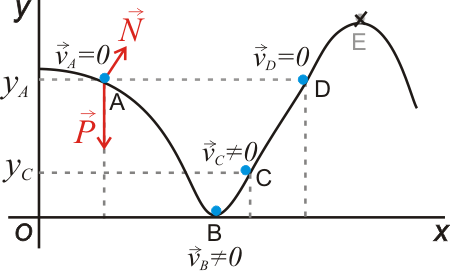
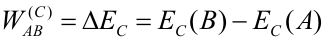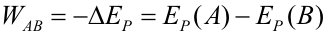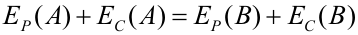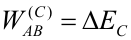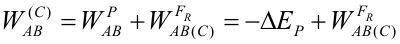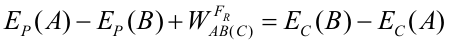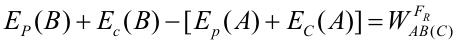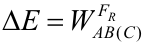Conservación de la energía mecánica

En el apartado de energía cinética hemos visto que el trabajo de una fuerza es igual a la variación de energía cinética que experimenta la partícula sobre la que actúa.

Esta expresión es válida para cualquier tipo de fuerza.

Por otra parte, para una fuerza conservativa:

Por tanto, para una fuerza conservativa podemos igualar las dos expresiones anteriores y, pasando al primer miembro lo que depende del estado inicial y al segundo lo del final:

La suma de la energía cinética y potencial de una partícula se denomina energía mecánica (E).

Si sobre una partícula actúan varias fuerzas conservativas, la energía potencial será la suma de las energías potenciales asociadas a cada fuerza.

La expresión anterior indica que, cuando sobre una partícula actúan únicamente fuerzas conservativas, su energía mecánica se conserva, esto es, permanece constante. Esta es la razón por la cual las fuerzas conservativas tienen este nombre: porque bajo la acción de dichas fuerzas la energía mecánica se conserva.

En la figura anterior se observa el movimiento de una partícula a lo largo de una pista sin rozamiento. La normal no hace trabajo por ser perpendicular a la trayectoria, de modo que la única fuerza que transfiere energía cinética a la partícula es el peso.

Como el peso es una fuerza conservativa, la energía mecánica de la partícula se conserva, por lo que la suma de su energía cinética y su energía potencial será la misma a lo largo de todo el recorrido.

En el punto A la partícula sólo tiene energía potencial (no tiene velocidad), mientras que en el punto B sólo tiene energía cinética, que será igual a la energía potencial en A. En cualquier otro punto de la trayectoria tendrá una combinación de ambas, pero de tal manera que la energía total es la misma en todos los puntos. El punto E no es alcanzable por la partícula, puesto que para llegar a él necesitaría más energía mecánica de la que tiene, pero la energía mecánica se conserva en esta situación.

Trabajo y energía cuando actúan fuerzas no conservativas

Cuando sobre la partícula actúan fuerzas conservativas y no conservativas, hay que utilizar la expresión que relaciona el trabajo con la variación de energía cinética, calculando el trabajo de cada fuerza y sumándolos todos. Si alguna fuerza es conservativa su trabajo se calculará como menos la variación de su energía potencial asociada, y de las demás habrá que calcular el trabajo aplicando la definición del mismo.

En la siguiente animación se muestra el movimiento de una masa que se desliza por un plano inclinado. Puedes variar el ángulo y el coeficiente de rozamiento. Observa cómo va variando la energía total (suma de potencial y cinética) para distintos coeficientes. ¿A dónde ha ido la energía que se pierde?

Cuando actúa la fuerza de rozamiento (no conservativa), habrá que proceder de la manera que se explica a continuación.

Partiendo de la expresión de la variación de energía cinética:

El trabajo del primer miembro es ahora la suma del trabajo del peso y del de la fuerza de rozamiento; el primero puede calcularse como menos la variación de la energía potencial gravitatoria, por lo que:

Lo que aparece en el primer término de esta ecuación es la variación de energía mecánica, por lo que finalmente queda: