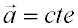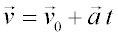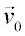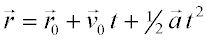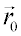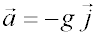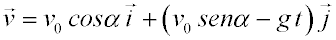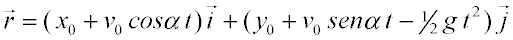Introducción (2/2)
Movimiento uniformemente acelerado:Cuando el vector aceleración es constante obtenemos por integración las siguientes ecuaciones para el vector velocidad y el vector posición en función del tiempo:
Un caso particular de este tipo de movimiento es el tiro parabólico, en el que un cuerpo se dispara con un cierto ángulo con respecto a la horizontal y cae bajo la acción de la gravedad. El vector aceleración tiene entonces sólo componente y, por lo que la componente x de la velocidad permanece constante. Las ecuaciones anteriores quedan así:
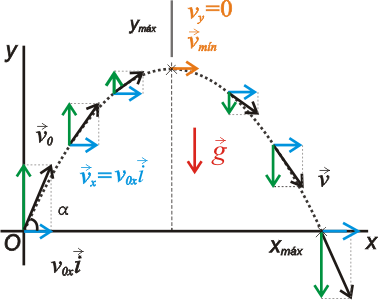
Si dibujamos la trayectoria en un sistema de ejes XY se obtiene una parábola. Se puede observar que en el punto más alto de la misma (ymáx) se anula la componente y
del vector velocidad ya que éste es siempre tangente a la trayectoria, por lo que la velocidad en ese instante toma su valor mínimo. Para calcular el alcance del proyectil (xmáx), se despeja el valor del tiempo igualando la coordenada y a cero, y se sustituye en la expresión de la coordenada x. En esta animación puedes cambiar el ángulo de lanzamiento y la masa del proyectil. El vector velocidad aparece en verde y sus componentes en rojo (vertical) y azul (horizontal). Se muestra también la altura máxima y el alcance del proyectil. |