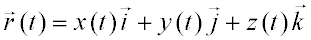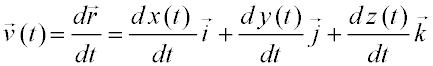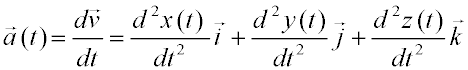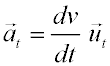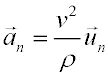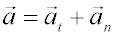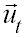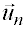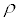Introducción (1/2)La cinemática es la parte de la mecánica clásica que estudia la descripción del movimiento de un cuerpo, sin atender a la causa que lo produce. Se limita esencialmente al cálculo de la trayectoria del cuerpo en función del tiempo. Para ello se debe utilizar un sistema de coordenadas, llamado sistema de referencia, constituido por tres ejes perpendiculares entre sí (ejes XYZ). Trataremos en todo este tema el movimiento de objetos puntuales (sin dimensiones). Definimos las magnitudes vectoriales vector posición, vector velocidad y vector aceleración, expresadas en componentes en función de los vectores unitarios de los ejes XYZ.
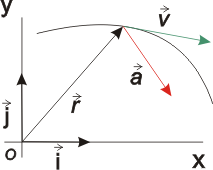
Las unidades respectivas de las magnitudes anteriores en el Sistema Internacional son: m, m/s y m/s2 En la siguiente figura están respresentados dichos vectores en dos dimensiones.
Componentes intrínsecas de la aceleración:En algunas ocasiones conviene usar un sistema de referencia cuyos ejes sean en cada instante tangente y normal a la trayectoria (no son fijos). Pincha sobre Tarzán y desplázalo de la posición de equilibrio, verás en la siguiente animación el movimiento oscilatorio de una masa y las componentes de su aceleración sobre el ejes tangente y el eje normal a la trayectoria. Definimos las componentes intrínsecas de la aceleración (aceleración normal y aceleración tangencial) como las componentes de la aceleración sobre este sistema de referencia. Se puede demostrar que dichas componentes valen:
A partir de las expresiones anteriores se puede deducir la interpretación física de cada una de estas componentes:
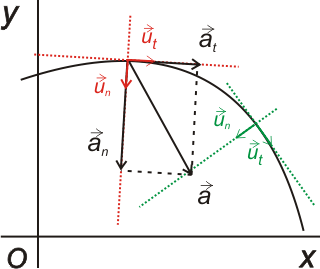
En la siguiente gráfica se han representado los vectores unitarios normal y tangente en dos puntos de la trayectoria y la descomposición del vector aceleración en sus componentes intrínsecas.
|
|||||||||||||||||||||||||||||||||