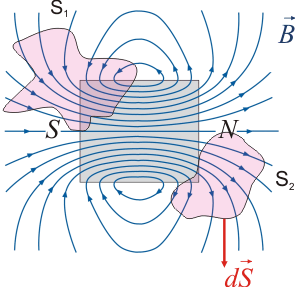
Flujo del campo magnético. Ley de Ampère

El flujo del campo magnético se define de manera análoga al flujo del campo eléctrico.

Flujo del campo magnético

El flujo del campo magnético Φ_m a través de una superficie se define:

donde dS es un vector perpendicular a la superficie en cada punto.

Como las líneas del campo magnético son cerradas (no existen monopolos), el flujo a través de cualquier superficie cerrada es nulo:

Por tanto, al contrario de lo que ocurría con la ley de Gauss, el flujo del campo magnético no puede emplearse para calcular campos magnéticos.

Ley de Ampère

La ley que nos permite calcular campos magnéticos a partir de las corrientes eléctricas es la Ley de Ampère. Fue descubierta por André - Marie Ampère en 1826 y se enuncia:

La integral del primer miembro es la circulación o integral de línea del campo magnético a lo largo de una trayectoria cerrada, y:

• μ₀ es la permeabilidad del vacío
• dl es un vector tangente a la trayectoria elegida en cada punto
• I_T es la corriente neta que atraviesa la superficie delimitada por la trayectoria, y será positiva o negativa según el sentido con el que atraviese a la superficie.

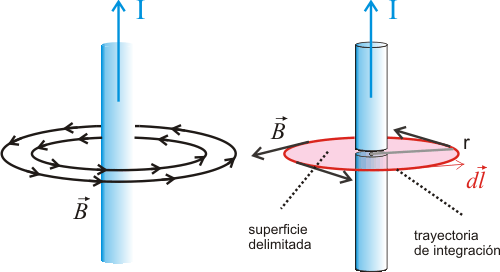
Campo magnético creado por un hilo infinito

Como aplicación de la ley de Ampère, a continuación se calcula el campo creado por un hilo infinito por el que circula una corriente I a una distancia r del mismo. Las líneas del campo magnético tendrán el sentido dado por la regla de la mano derecha para la expresión general del campo creado por una corriente, por lo que sus líneas de campo serán circunferencias centradas en el hilo, como se muestra en la parte izquierda de la siguiente figura.

Para aplicar la ley de Ampère se utiliza por tanto una circunferencia centrada en el hilo de radio r. Los vectores y dl son paralelos en todos los puntos de la misma, y el módulo del campo es el mismo en todos los puntos de la trayectoria. La integral de línea queda:

Empleando la ley de Ampère puede calcularse el campo creado por distintos tipos de corriente. Dos ejemplos clásicos son el del toroide circular y el del solenoide ideal (*), cuyos campos se muestran en la siguiente tabla.

Toroide circular Solenoide ideal*

(*) Un solenoide ideal es una bobina de longitud grande cuyas espiras están muy juntas. En la expresión del campo magnético que crea, n es el número de espiras por unidad de longitud.