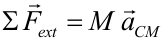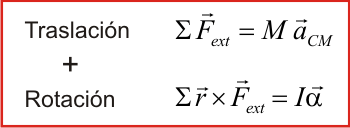Rotación con respecto al centro de masasCuando el eje de rotación de un sólido no está fijo, su movimiento será una combinación de rotación y traslación, como está descrito en la introducción. En este caso, para describir el movimiento son necesarias dos ecuaciones: una que nos permita calcular la aceleración de su centro de masas y otra que nos dé su aceleración angular con respecto a un eje que pasa por el centro de masas. La primera de ellas es la segunda ley de Newton aplicada a un sistema de partículas:
Y la segunda es la ecuación del movimiento de rotación pero referida al centro de masas del sólido. Para obtener esta ecuación hay que derivar el momento angular interno del sólido, obteniendo:
donde la prima (') denota que los momentos de las fuerzas externas están calculados con respecto al centro de masas, y α' es la aceleración angular del sólido con respecto a un eje que pasa por el centro de masas. En el siguiente cuadro se resume el modo de analizar el movimiento de un sólido rígido:
Equilibrio estáticoUna aplicación directa de las ecuaciones anteriores es la estática, cuyo objetivo es determinar bajo qué condiciones un sistema se encuentra en reposo. Su aplicación más importante es al cálculo de estructuras, donde se emplea para determinar las fuerzas soportadas por un puente, un edificio, una viga, un rascacielos, etc. Para que un cuerpo esté en equilibrio estático deben cumplirse simultáneamente dos condiciones:
Estas dos condiciones se imponen respectivamente a la ecuación del movimiento de traslación del centro de masas (segunda ley de Newton) y a la ecuación de la rotación:
La segunda condición se cumple con independencia del origen que se elija para calcular los momentos de las fuerzas externas (demostración). Resolviendo el sistema de ecuaciones anterior se calculan las fuerzas que actúan sobre el sistema en equilibrio. En esta animación se tiene una viga en equilibrio unida a la pared mediante una articulación. Puedes pinchar sobre la viga y variar su ángulo de inclinación y también desplazar la masa a lo largo de la viga. Observa cómo varían las reacciones en la articulación y la tensión de la cuerda. |