Ciclo de Carnot

En principio, cualquier ciclo termodinámico se puede utilizar para diseñar una máquina o un refrigerador, según el sentido en el que se recorra el ciclo. Puesto que, según el enunciado del Segundo Principio ninguna máquina puede tener rendimiento 100%, es importante saber cuál es el máximo rendimiento posible entre dos focos determinados. Como veremos, el ciclo de Carnot proporciona ese límite superior entre dos focos. Este ciclo es una idealización ya que está constituido por transformaciones reversibles: el intercambio de calor de la sustancia de trabajo con los focos se produce a través de isotermas y las variaciones de temperatura de forma adiabática, para que no haya pérdidas de calor.

A continuación estudiaremos este ciclo para máquinas y para refrigeradores, considerando siempre que la sustancia de trabajo es un gas ideal.

Máquina de Carnot

En una máquina el ciclo se recorre en sentido horario para que el gas produzca trabajo. Las transformaciones que constituyen el ciclo de Carnot son:

• Expansión isoterma (1-2): al gas absorbe una cantidad de calor Q₁ manteniéndose a la temperatura del foco caliente T₁.
• Expansión adiabática (2-3): el gas se enfría sin pérdida de calor hasta la temperatura del foco frío T₂.
• Compresión isoterma (3-4): el gas cede el calor Q₂ al foco frío, sin variar de temperatura.
• Compresión adiabática (4-1): el gas se calienta hasta la temperatura del foco caliente T₁, cerrando el ciclo.

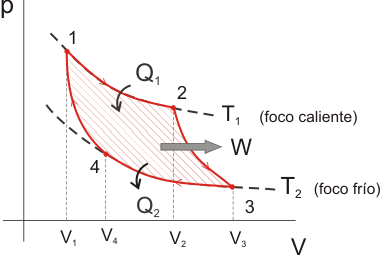Calculando el trabajo en las transformaciones isotermas: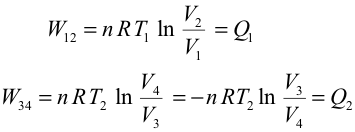

y dividiendo entre sí las expresiones de las variables de estado en las adiabáticas obtenemos la siguiente relación para los volúmenes: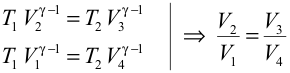

El rendimiento para una máquina de Carnot será entonces: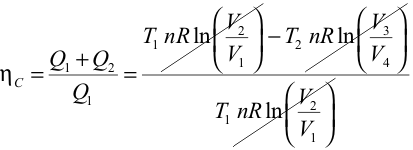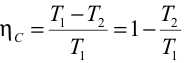

Es decir, sólo depende de las temperaturas de los focos. Este rendimiento es mayor cuanto mayor sea la diferencia de temperaturas entre los focos y es siempre menor que uno, ya que ni T₂ puede ser nula ni T₁ infinito.

Refrigerador de Carnot

El ciclo se recorre en sentido antihorario, ya que el trabajo es negativo (trabajo consumido por el gas):

• Expansión adiabática (1-2): el gas se enfría sin pérdida de calor hasta la temperatura del foco frío T₂.
• Expansión isoterma (2-3): el gas se mantiene a la temperatura del foco frío (T₂) y durante la expansión, absorbe el calor Q₂ de dicho foco.
• Compresión adiabática (3-4): el gas se calienta hasta la temperatura del foco caliente T₁, sin intercambio de calor.
• Compresión isoterma (4-1): al gas cede el calor Q₁ al foco caliente, manteniéndose a la temperatura de dicho foco T₁ y cerrando el ciclo.

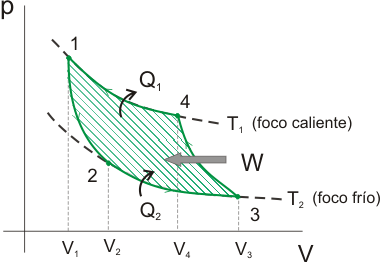Mediante un procedimiento análogo al anterior y recordando la definición de eficiencia de un refrigerador, se llega para el refrigerador de Carnot a la expresión: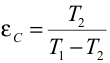

Teorema de Carnot

El teorema de Carnot es una consecuencia de que todas las transformaciones son reversibles, por lo que intuitivamente se deduce que ninguna máquina podrá funcionar mejor, es decir, tendrá mayor rendimiento.

Ninguna máquina funcionando entre dos focos térmicos tiene mayor rendimiento que el de una máquina de Carnot operando entre dichos focos. Todas las máquinas reversibles que operen entre dos focos poseen el mismo rendimiento, dado por el de Carnot.

Como en la práctica siempre existe algún grado de irreversibilidad, el rendimiento de Carnot proporciona un límite superior para el valor del rendimiento, conocidas las temperaturas de los focos, independientemente de cómo se construya la máquina, de la sustancia de trabajo, etc.