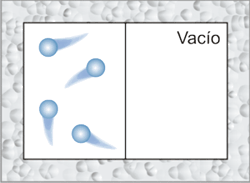
Definición microscópica de entropíaTodas las magnitudes definidas a lo largo de estas páginas se han introducido desde el punto de vista macroscópico; es decir, en ningún momento se ha tenido en cuenta la naturaleza molecular de la materia. La entropía no ha sido una excepción a esta regla. La parte de la Física que se ocupa de estudiar las propiedades termodinámicas de un sistema relacionándolas con el comportamiento microscópico del mismo se denomina termodinámica estadística. Para ver un ejemplo de cómo se relaciona el comportamiento microscópico de un sistema con su comportamiento macroscópico, vamos a analizar la expansión libre de Joule desde el punto de vista de las moléculas que constituyen el gas. En el siguiente dibujo se ha representado un sistema aislado: un gas encerrado en un recipiente. Para simplificar, el gas representado está constituido por cuatro moléculas; sin embargo hay que tener en cuenta que los sistemas reales poseen un número mucho mayor de partículas. El gas se encuentra en el compartimento de la izquierda, y en el derecho está hecho el vacío.
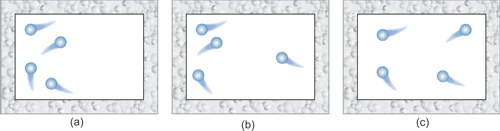
Cuando se elimina la pared que separa ambos compartimentos, la experiencia nos dice que el gas tiende a ocupar todo el volumen disponible. En principio, sin embargo, cualquiera de las configuraciones representadas en la figura inferior sería posible. Dichas configuraciones se denomiman macroestados del sistema.
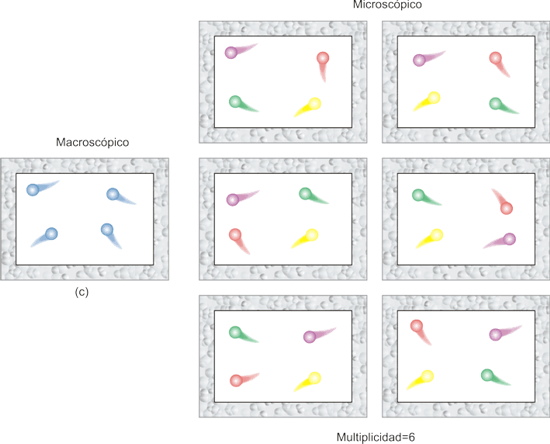
Para un macroestado determinado, las moléculas que constituyen el gas pueden a nivel microscópico (en nuestro ejemplo, asignando distintos colores a las moléculas) distribuirse según diferentes configuraciones, denominadas microestados. La multiplicidad es el número de microestados que conducen al mismo estado macroscópico (macroestado) de un sistema. De todos los macroestados representados en la figura anterior, el (c) tiene mayor multiplicidad, ya que a nivel microscópico, las moléculas pueden adoptar las siguientes configuraciones:
A finales del siglo XIX, el físico austriaco Ludwig Boltzmann definió la entropía como:
donde k es la constante de Boltzmann (k = 1.3806504 × 10-23 J K-1 ) y &Omega es el número de microestados accesibles a un macroestado dado. La configuración (c) representada en la figura anterior es la que más microestados accesibles tiene y por tanto es la de mayor entropía. El sistema tratado en este ejemplo tenderá a estar en esta configuración porque es la que mayor entropía tiene. La ecuación de la entropía se encuentra grabada en la tumba de Boltzmann en Viena. |