Problemas resueltos (2/3)


4.- En un espectáculo al aire libre de saltos acrobáticos, un ciclista ensaya sobre la pista de la figura de manera que sale despedido con una velocidad vo = 15 m/s desde la rampa inclinada un ángulo α = 30o y una altura h1 = 3 m. Quiere aterrizar sobre una plataforma de altura h2 = 1.5 m.





  1. Expresar las componentes del vector posición y del vector velocidad en función del tiempo. Calcular la máxima altura alcanzada por el ciclista y la velocidad en ese instante. (Pincha para ver el resultado).
  2. ¿A que distancia, como máximo, se tiene que colocar la plataforma para que caiga sobre ella? (Pincha para ver el resultado).

El día del concurso existe viento que provoca una aceleración horizontal de frenado.

  1. Razonar cómo cambian las respuestas del apartado (a). (Pincha para ver el resultado).
  2. Calcular cuánto vale la aceleración provocada por el viento si para que aterrice sobre ella habría que adelantar la plataforma 1.3 m con respecto a la distancia del apartado (b). (Pincha para ver el resultado).
Resolución del problema en pdf



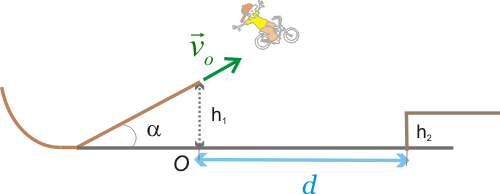
5.- Una atracción de feria consiste en un muñeco que sube por un carril a una velocidad constante de 2 m/s. Desde una distancia d se dispara un proyectil con una velocidad inicial de 15 m/s y un ángulo de inclinación de 30o. En el instante del disparo el proyectil se encuentra a una altura de 1.28 m por encima del muñeco.




  1. Expresar en forma vectorial la velocidad y la posición inicial del proyectil, así como la aceleración a la que está sometido durante el vuelo. (Pincha para ver el resultado).
  2. Expresar en componentes la velocidad y la posición del proyectil en función del tiempo. (Pincha para ver el resultado).
  3. Determinar la distancia d a la que se tiene que situar la pistola para que el proyectil alcance al muñeco. (Pincha para ver el resultado).
  4. Calcular el módulo de la aceleración tangencial en el instante en el que proyectil alcanza al muñeco. (Pincha para ver el resultado).
Resolución del problema en pdf



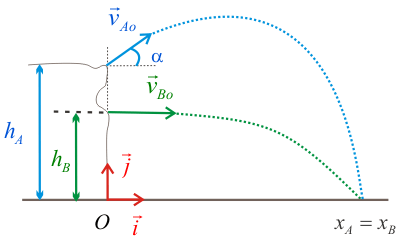
6.- Un niño A está en lo alto de un barranco de altura hA = 40 m y lanza una piedra con una velocidad vAo = 24 m/s y un ángulo α = 30o. Su amigo B se encuentra por debajo de él sobre la misma vertical a una altura hB del suelo y lanza otra piedra horizontalmente con una velocidad vBo = 36.5 m/s. ¿Cuánto vale hB si las dos piedras llegan al mismo sitio en el suelo?


  1. Calculamos el tiempo que tarda en caer el proyectil A y la distancia xA a la que cae (Pincha para ver el resultado).
  2. Imponemos que el proyectil B caiga en el mismo sitio (xB = xA) (Pincha para ver el resultado).
Resolución del problema en pdf