Condición de rodadura

Cuando un sólido rota a la vez que se traslada describir el movimiento con respecto a un SR inercial puede ser una tarea ardua, pero se simplifica si el sólido realiza lo que se conoce como rodadura, es decir, que gira sin deslizar. En este caso que existe una condición de ligadura que relaciona la velocidad con la que se traslada el CM y la velocidad angular de rotación del sólido. En una rodadura el punto de apoyo del sólido (por ejemplo, una esfera apoyada en un suelo horizontal) no sufre desplazamiento con respecto al suelo, o lo que es lo mismo, está instantáneamente en reposo.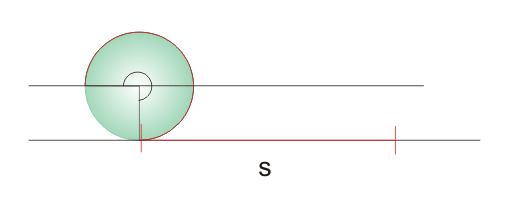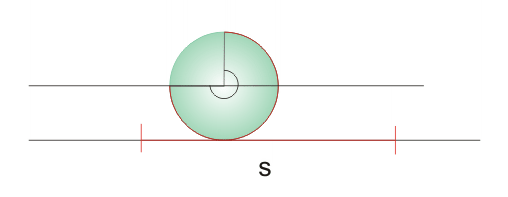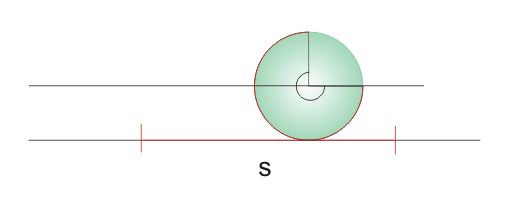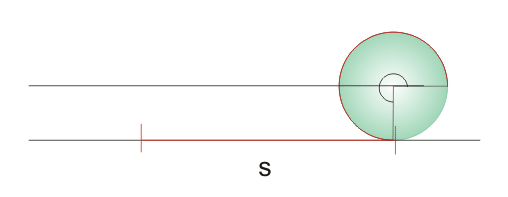

Supongamos una esfera apoyada en el suelo. Para que ruede debe haber alguna fuerza que haga momento con respecto al CM, según la ecuación de la dinámica de rotación, por ejemplo, una fuerza de rozamiento, ya que ni el peso ni la normal ejercen momento con respecto al CM.

Para que la esfera ruede sin deslizar, el desplazamiento del CM debe coincidir con el arco s correspondiente al ángulo girado, según se aprecia.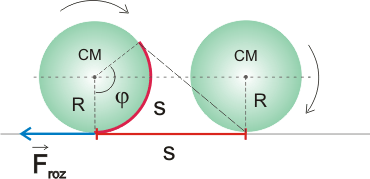

La velocidad con la que se traslada el CM será la derivada con respecto al tiempo de dicho desplazamiento: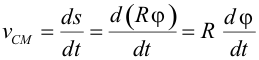

Puesto que la variación del ángulo girado es la velocidad angular de rotación ω, se tiene finalmente que: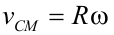

Esta expresión es la condición de rodadura y nos da la relación que debe haber entre la velocidad de traslación del CM y la velocidad angular de rotación para que el sólido ruede sin deslizar.

Si derivamos, se obtiene la relación entre las aceleraciones: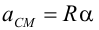

En esta animación puedes ver las velocidades del CM (en rojo) y de un punto del borde (en azul), medidas por un observador en reposo, para una rodadura y para un deslizamiento de la esfera. También se puede representar para cada caso la trayectoria de un punto del borde.

Fuerza de rozamiento en una rodadura

La fuerza de rozamiento puede ser la causante de que un objeto ruede, pero ¿por qué nos cuesta menos desplazar un objeto haciéndolo rodar que deslizarlo sobre el suelo? Veamos una explicación.

El movimiento de rodadura de un sólido rígido se puede descomponer en un movimiento de rotación con respecto a un eje que pase por el CM y un movimiento de traslación. En la rotación las partículas del borde describen un movimiento circular con una velocidad lineal v = Rω con respecto al CM; a su vez éste se traslada con una velocidad v_CM = Rω con respecto al suelo (condición de rodadura). Luego la velocidad del punto de apoyo con repecto al suelo es nula, ya que se cancelan ambas, lo que confirma que no se produce deslizamiento.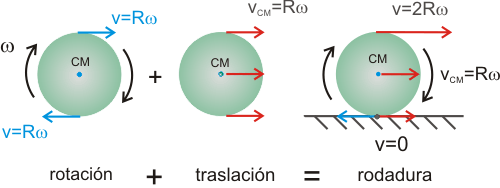

Aplicando la definición de trabajo a la fuerza de rozamiento, se observa que como no hay desplazamiento el trabajo que realiza la fuerza de rozamiento sobre el punto de apoyo es nulo, por lo que:

En una rodadura la fuerza de rozamiento no disipa energía

Otra consecuencia importante es que el módulo de la fuerza de rozamiento debe obtenerse de las ecuaciones del movimento, ya que al no haber desplazamiento relativo entre las superficies en contacto, no toma el valor del coeficiente cinético por la normal.

En una rodadura el módulo de la fuerza de rozamiento no es μcN